My Sunday afternoon project wasn't something that I could just let lie and it didn't take long for work to start on it again. Using the list of improvements I had identified, I began with the aesthetics and then moved on to other, more number intensive areas of research.
Before even touching the code I subsumed everything into a Git repository; I'm a long time Subversion user but relatively new to Git so I still regularly refer back to the "Git - SVN Crash Course" which is pleasantly concise. With this done, I attacked the GIF output method first:
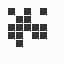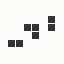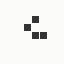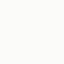
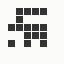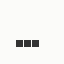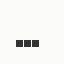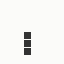
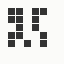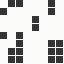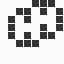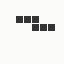
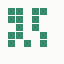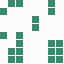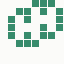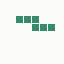


The generation was done by using different parts of the e-mail address again: the full address for the red component, the local part for the green component and the domain part for the blue component. This method produced the first four images and had a definite tendency for the green spectrum again, I then altered it slightly to compute the red component from the local part and green from the full address which resulted in a pleasing orange colour. Next was to try to tone down the rapid movement - while a tenth of second is fine for debugging and tracking progression, it's distracting when viewed for long periods of time and the possibility of multiple avatars appearing at the same time meant slowing down the animation:
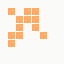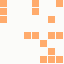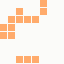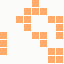
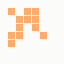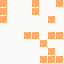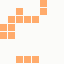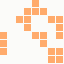
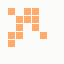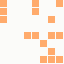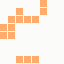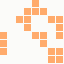
The first is the original 1/10 of a second, the second is 1/2 and the third 3/4. Obviously when viewed next to quicker varieties the effect is somewhat lost, but at 3/4 of a second per frame, a full fifty generations will last close to a minute and still remain under 15k/b which is more than acceptable for an avatar. Performing a full run on the original 1,300+ e-mail addresses, produced a set of results which coincidentally matched my previous desire to be able to identify an e-mail address's domain at a glance. For example, Hotmail tended towards greens and oranges:


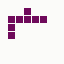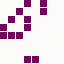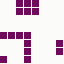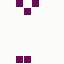




while BT Internet more towards blues and pale yellows:
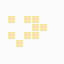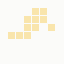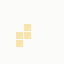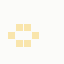



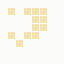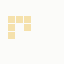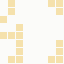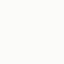


These are regardless of the local part of the address, and while they're not the "one colour per domain" that I had hoped for, in aggregate their identity is clear.
In a sense, that was the project completed, I had created something that was unique, quirky and most of all aesthetically pleasing; I could spend hours tweaking and adjusting parameters to make for better avatars, perhaps slowing down the animation further or altering the colour generation methods, but for what it is, the result is better than I expected. This wasn't the end of the work though. As you may notice, none of the above animations have any protracted dead states, whereby the animation is blank or static for more than a frame - the reason for this is that while I addressed the aesthetics first, I also implemented two heuristics to stop the algorithm in those cases:
private function isInactive(array $state)
{
foreach($state AS $row)
{
foreach($row AS $cell)
{
if($cell == 1)
{
return false;
}
}
}
return true;
}
private function isEqual(array $state1, array $state2)
{
foreach($state1 AS $h => $row)
{
if($row !== $state2[$h])
{
return false;
}
}
return true;
}
Both are simple and are called after a new state has been generated and output but before it has been switched for the current state, that way the final state will still be shown but no further operations will take place. These both cover the most common cases but ignores more specialised examples such as patterns with an alternating pattern (period two or above) which will not be caught. The inactivity function could be ignored altogether and rely on the equality function but this would require at least two generations of dead cells which I deemed to be unacceptably. Both of these functions are the result of optimisations meant to short-circuit generation and prevent needless calculation. However I wasn't entirely certain that the cost of iterating through the grid was worth it, so storing away the timings for the original version of the algorithm I did a number of other benchmarks to see whether this was worth it, and to get some general statistics on the process.
Statistics
The first run used the first version of the algorithm (no stop checks) on a 32x32 grid over 50 generations on 1382 sample e-mail addresses. The average time for only the game to run (e.g. not counting the seed or colour generation) including GIF generation was 1.2227 seconds; with a standard deviation of 0.0623 and variance of 0.0039, the numbers are fairly solid. On an identical run but including stop checks the average time per run was 0.6297 seconds, while standard deviation and variance were 0.5097 and 0.2598 respectively - obviously the shorter average time is balanced out by the distribution of values, the quickest run finished in 0.0352 seconds while the slowest came out at 1.8953. I wanted the values to be as "real world" as possible which is why I didn't bother checking for the time taken to process all values or take more detailed timings from within the Life algorithm itself, these numbers represent values likely to be experienced if this was to ever be put into use.
This proved that pruning was worthwhile overall, so I continued on with some comparative testing. Using the same sample set and generation count, an 8x8 grid had an average time per run of 0.3078 seconds while a 64x64 grid average 1.4124 seconds which is still only slightly worse than a 32x32 without any stop state checking. It's difficult to tell with only three data points how exactly the algorithm is going to increase in time versus grid size but the correlation if it wasn't obvious before is backed up by the statistics.
With these checked, I moved on to the other secondary aspects of the algorithm, namely the colour and seed generation. I was interested in both how long they took to run and also the quality of the results they produced: namely whether there were any collisions in the colours and seeds. For the original two colour generation from an e-mail address, the time taken was tied to the length of the string being operated on, even so the average time taken was ~0.0001 for strings up to 39 characters long which meant this wasn't a very computationally expensive operation. The most five common string lengths were between 20 and 25 characters long:
| String length | Average time | Standard deviation | Variance | Count |
|---|---|---|---|---|
| 20 | 9.30851E-05 | 1.44625E-05 | 2.09163E-10 | 94 |
| 21 | 9.37708E-05 | 1.56694E-05 | 2.45531E-10 | 96 |
| 22 | 0.000101972 | 1.91865E-05 | 3.68121E-10 | 107 |
| 23 | 0.000102602 | 1.78043E-05 | 3.16992E-10 | 133 |
| 24 | 0.00010361 | 1.86302E-05 | 3.47085E-10 | 118 |
| 25 | 0.000108533 | 2.64901E-05 | 7.01723E-10 | 137 |
Not exactly thrilling reading but demonstrates that it was running much as I expected. What was most worrying was when I checked for collisions for each colour (background and foreground): 43 foreground collisions and 83 background collisions and 43 full colour collisions; all of the e-mail addresses were unique so this was a worrying trend. I was particularly concerned with the background colour but even with such a small sample set (in comparison to the number of possible e-mail addresses) there is a 3.1% chance of a full collision which is less than ideal. The one colour generation fared little better:
| String length | Average time | Standard deviation | Variance | Count |
|---|---|---|---|---|
| 20 | 0.00010434 | 1.68583E-05 | 2.84203E-10 | 94 |
| 21 | 0.000108323 | 1.69948E-05 | 2.88823E-10 | 96 |
| 22 | 0.000112514 | 1.34494E-05 | 1.80885E-10 | 107 |
| 23 | 0.000111835 | 1.68996E-05 | 2.85597E-10 | 133 |
| 24 | 0.000114466 | 1.76485E-05 | 3.11469E-10 | 118 |
| 25 | 0.000120416 | 1.49733E-05 | 2.24199E-10 | 137 |
Not only is it marginally slower but the number of collisions came to 147 which is 10.6% of the sample set, worse than the two colour generation and odd considering the range of colours that this function can produce. The key is in the standard deviation of the colours though: 73.9285, 72.4408, 75.2587 for the red, green and blue components - despite using most of the colour spectrum, they don't deviate much from the mean which is increasing the likelihood of a collision.
While there are equally detailed statistics for the seed generation, the number show much of what one would expect: time increases according to string length and general time, like the colour generation is in the region of ~0.0001 seconds for average length addresses. What I was most interested in though is the number of identical seeds: 22. This is not entirely unexpected given that the method for generating was cooked up in a few hours and wasn't subject to any stringent mathematical basis, 1.6% of the sample set isn't game breaking.
All of this may seem academic for such a small system but the results are invaluable if I ever wanted to advance the script any - the statistics show that the further optimisation of the Life algorithm could yield quicker run times, while the seed and colour generation need work to be able to generate more unique values. The Life algorithm is well travelled by other programmers which means a lot of the complex optimisation work has already been done (Hash Life etc.) whereas the two generators definitely need more work and a more structured approach to their construction.
Release
For the moment I'm finished tinkering with the algorithm itself so it makes sense to release the code in case anyone else wishes to use this as a base. The license for this release is Creative Commons Attribution-Share Alike 3.0 which means you can download, redistribute, play and alter but give credit where it's due. This is version 1.1 which includes the checks for stop conditions.
Conway's Game of Life in PHP + Seed and Colour generation - version 1.1
ZIP - 7kb